有重复的排列组合问题：

从n个元素中选出m个可重复的元素，一共有多少组合？

思路：建立一个映射，使m个可重复的元素变成m个不可重复的元素，再使用公式。

具体来说，原始的m个元素的编号取值区间为1<x<n. 通过映射:
$x$: $x_1$, $x_2$, $x_3$, …, $x_m$
$f(x)$: $x_1$+0, $x_2$+1, $x_3$+2, …, $x_m$+m-1
使得新的m个元素的编号取值区间为1<x<(n+m-1)，一一对应并且元素不再重复，所以组合数为$C_{n+m-1}^m$.

从n个元素中选出m个可重复的元素，并排序，一共有多少序列？

是$n^m$，还是$A_{n+m-1}^m$，思考一下。

从n个元素中选出m个可重复的元素，并排成一个圆，旋转算作重复，一共有多少组合？

从n个元素中选出m个可重复的元素，并排成一个圆，旋转+反转均算作重复，一共有多少组合？

何必等明天，从今天开始坚持写工作日志。

Introduction

Within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed occurs where the pressure is highest. Why?

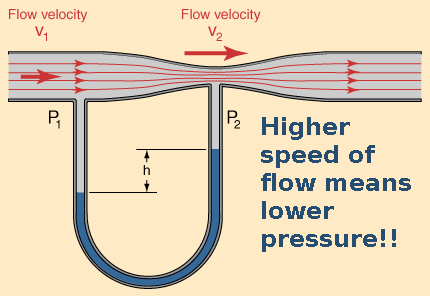
In fluid mechanics, Bernoulli’s principle states that, in a steady flow, the sum of all forms of energy in a fluid () along a streamline remains constant. The forms of energy involves the kinetic energy, the potential energy and the internal energy. Bernoulli’s principle can also be derived directly from Newton’s Second Law of Motion.

谢道韫，字令姜，生卒年不详，东晋（317年4月6日－420年7月10日）时期有名的才女，典型的白富美。韫有收藏，蕴藏之意，如「石韫玉而山辉，水怀珠而川媚」。

谢道韫有不少有名的典故。《世说新语•言语》中记载了这么一个故事：

Introduction

PDE can be classified as elliptic, parabolic or hyperbolic. In fluids dynamics, the governing equations contain first and second derivatives in the spatial coordinates and first derivatives only in time. The spatial derivatives often appear nonlinearly while the time derivatives appear linearly. For linear PDE of second-order in two independent variables $x$ and $y$,

$A\frac{\partial^2 u}{\partial x^2} + B\frac{\partial^2 u}{\partial x \partial y} + C\frac{\partial^2 u}{\partial y^2} + D\frac{\partial u}{\partial x} + E\frac{\partial u}{\partial y} + Fu + G =0$

A simple classification is as follows.

Introduction

A boundary layer refers to the layer of fluid in the immediate vicinity of a bounding surface where the effects of viscosity are significant [1]. Proposed by Ludwig Prandtl, the flow past a body can be divided into two regions: a very thin layer close to the body (boundary layer) where the viscosity is important, and the remaining region outside this layer where the viscosity can be neglected [2]. Since the inviscid flow solution does not satisfy the no-slip condition at the wall, boundary-layer theory is called a singular perturbation method.

The transition from laminar flow to turbulent flow was first examined in pipe flow by O. Reynolds (1883). Prandtl’s comprehensive contribution appeared in Aerodynamic Theory, edited by W.F. Durand, L. Prandtl (1935). A separation of the boundary layer from the body and the formation of large or small eddies at the back of the body can then occur. This kind of separation could be detrimental.

Laminar and turbulent flow

What is RANS

The Reynolds-averaged Navier–Stokes equations (RANS equations) for the three-dimensional incompressible viscous flow consists of the continuity equation and the momentum equations as follows:

$\frac{\partial u_i}{\partial x_i} = 0$

$\rho \frac{\partial u_i}{\partial t} + \rho u_j \frac{\partial u_i}{\partial x_j} = -\frac{\partial p}{\partial x_i} + \frac{\partial}{\partial x_j} \left[ \mu \left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \right] + \frac{\partial}{\partial x_j} (-\rho \overline{u'_i u'_j})$

where $u_i$, i=1,2 in two-dimensional flow, denotes the velocity components along x-,y-axis, respectively. $p$ is the pressure. $rho$ is the water density. $\mu$ is the dynamic viscosity of water. $-\rho \overline{u'_i u'_j}$ are the Reynolds stresses or the apparent turbulent shear stress.

Turbulence Modeling

The Reynolds stresses can be solved based on the Boussinesq hypothesis using the eddy viscosity turbulence models, or be solved from the transport equation based on Reynolds stress models. In the present studies, one-equation and two-equation eddy viscosity models as well as Reynolds stress models were employed to solve the RANS equations.

In the eddy viscosity models, it is assumed that the Reynolds stresses are related to the mean velocity gradients, the turbulence kinetic energy and eddy viscosity, i.e.,

$-\rho \overline{u'_i u'_j} = \mu_t \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) - \frac{2}{3}(\rho k + \mu_t \frac{\partial u_i}{\partial x_i}) \delta_{ij}$

where $\mu_t$ represents the eddy viscosity, $\delta_{ij}$ is the Kronecker delta, $k=\frac{1}{2}\overline{u'_i u'_j}$ is the turbulent kinetic energy that can be solved from the transport equations. The Reynolds stress tensor is linearly proportional to the mean strain rate. Note that the term $\frac{\partial u_i}{\partial x_i}$ equals to zero for incompressible flows.

The simple one-equation model, Spalart-Allmaras (SA) model is implemented. The SA turbulence model solves a transport equation for the modified diffusivity $\tilde{\nu}$ to determine the turbulence eddy viscosity, $\mu_t$, i.e.,

$\mu_t=\rho f_{\nu 1} \tilde{\nu}$

where $f_{\nu 1}$ is a damping function. The transport equation for the modified diffusivity is:

$\frac{\partial}{\partial t} (\rho \tilde{\nu}) + \nabla \cdot (\rho \tilde{\nu} \bar{v}) = \frac{1}{\sigma_{\tilde{\nu}}} \nabla \cdot [(\mu + \rho \tilde{\nu}) \nabla \tilde{\nu}] + P_{\tilde{\nu}} + S_{\tilde{\nu}}$

where $\bar{v}$ is the mean velocity, $\sigma_{\tilde{\nu}}$ is a model coefficient, $\mu$ is the dynamic viscosity, $P_{\tilde{\nu}}$ is the production term and $S_{\tilde{\nu}}$ is the source term. SA model has good convergence and robustness for specialized flows. However, the turbulence length and time scales are not well defined as they are in other two-equation models.

Two-equation models are widely used solve the RANS equations, in which both the velocity and length scale are solved using separate transport equations. The turbulence length scale is estimated from the kinetic energy and its dissipation rate. The standard $k-\epsilon$, standard $k-\omega$ and the Shear Stress Transport (SST) $k-\omega$ models are investigated.

In the $k-\epsilon$ model, the turbulent eddy viscosity is calculated as:

$\mu_t=\rho C_{\mu}f_{\mu} kT$

where $C_{\mu}$ is a model coefficient, $f_{\mu}$ is a damping function and $T$ is the turbulent time scale, which is calculated as:

$T = \max(T_e,C_t\sqrt{\frac{\nu}{\epsilon}})$

where $T_e=\frac{k}{\epsilon}$ is the large-eddy time scale, $C_t$ is a model coefficient, $\nu$ is the kinematic viscosity. The transport equations for the turbulent kinetic energy $k$ and the turbulence dissipation rate $\epsilon$ are written as:

$\frac{\partial}{\partial t} (\rho k) + \nabla \cdot (\rho k \bar{v}) = \nabla \cdot \left[ (\mu + \frac{\mu_t}{\sigma_k}) \nabla k \right] + P_k -\rho(\epsilon-\epsilon_0) + S_k$

$\frac{\partial}{\partial t} (\rho \epsilon) + \nabla \cdot (\rho \epsilon \bar{v}) = \nabla \cdot \left[ (\mu + \frac{\mu_t}{\sigma_{\epsilon}}) \nabla \epsilon \right] + \frac{1}{T_e} C_{\epsilon 1} P_{\epsilon} - C_{\epsilon 2} f_2 \rho(\frac{\epsilon}{T_e}-\frac{\epsilon_0}{T_0}) + S_{\epsilon}$

where $\sigma_k$, $\sigma_{\epsilon}$, $C_{\epsilon 1}$ and $C_{\epsilon 2}$ are model coefficients, $P_k$ and $P_{\epsilon}$ are production terms, $f_2$ is a damping function, $S_k$ and $S_{\epsilon}$ are source terms. In the realizable $k-\epsilon$ model, the equation for turbulence dissipation rate is modified and the coefficient $C_{\mu}$ is expressed as a function of mean flow and turbulence properties instead of constant in the standard model. The effect of the mean flow distortion on turbulent dissipation is introduced to improve the performance for rotation and streamline curvature. It also improves the boundary layer under strong adverse pressure gradients or separation. The renormalization group (RNG) $k-\epsilon$ model is based on renormalization group analysis of the Navier-Stokes equations. Different constants are used in the transportation equations for the turbulence kinetic energy and dissipation. The RNG $k-\epsilon$ model leads to lower turbulence levels and generated less viscous flows.

In the $k-\omega$ model, the turbulent eddy viscosity is related to the turbulence kinetic energy, $k$, and the specific turbulence dissipation rate, $\omega$, which is also referred to the mean frequency of the turbulence. The turbulent eddy viscosity is calculated as:

$\mu_t=\rho kT$

where $T=\frac{\alpha^*}{\omega}$ is the turbulence time scale in the standard $k-\omega$ model. $\alpha^*$ is a model coefficient. The transport equations for the turbulent kinetic energy $k$ and the specific dissipation rate $\omega$ are written as:

$\frac{\partial}{\partial t} (\rho k) + \nabla \cdot (\rho k \bar{v}) = \nabla \cdot \left[ (\mu + \sigma_k \mu_t) \nabla k \right] + P_k -\rho \beta^*f_{\beta^*}(\omega k - \omega_0 k_0) + S_k$

$\frac{\partial}{\partial t} (\rho \omega) + \nabla \cdot (\rho \omega \bar{v}) = \nabla \cdot \left[ (\mu + \sigma_\omega \mu_t) \nabla \omega \right] + P_\omega -\rho \beta f_{\beta}(\omega^2 - \omega_0^2) + S_k$

where $\sigma_k$, $\sigma_{\omega}$ are model coefficients, $P_k$ and $P_{\omega}$ are production terms, $f_{\beta^*}$ is the free-shear modification factor.is the vortex-stretching modification factor, $k_0$ and $\omega_0$ are the ambient turbulence values that counteract turbulence decay, $S_k$ and $S_{\omega}$ are source terms. The $k-\omega$ model predicts strong vortices and the near-wall interactions more accurately than the $k-\epsilon$ models. The limitations of the original $k-\omega$ model include the over-prediction of shear stresses of adverse pressure gradient boundary layers, and the sensitivity to initial conditions and inlet boundary conditions.

For the SST $k-\omega$ model, the transport equations are the same as those of the standard $k-\omega$ model by setting the damped cross-diffusion derivative term as zero in the near region. In the far field, the transport equations are the same as those of the standard $k-\epsilon$ model, which can avoid the problem that the model is too sensitive to the inlet turbulence properties. Detailed formulations can be found in the work by Menter (1993). The SST $k-\omega$ model introduces the transport of the turbulence shear stress and improves the prediction of the onset and the flow separation under adverse pressure gradients.

In the Reynolds stress models (RSM), the transport equations are solved for all the components of the Reynolds stress tensor and the turbulence dissipation rate, i.e.,

$\frac{\partial}{\partial t} (\rho \overline{u'_i u'_j}) + \frac{\partial}{\partial x_k} (\rho u_k \overline{u'_i u'_j} ) = P_{ij} + F_{ij} + D_{ij}^T + \phi_{ij} - \epsilon_{ij}$

where $P_{ij}$ is the stress production, $F_{ij}$ is the rotation production, $D_{ij}^T$ is the turbulent diffusion, $\phi_{ij}$ is the pressure strain tensor and $\epsilon_{ij}$ is the dissipation rate tensor. The isotropic turbulent dissipation rate is solved from a transport equation analogous to the $k-\epsilon$ model with various model coefficients.

In order to resolve the viscous sublayer, two RSM models can be implemented, including the elliptic blending model (EB-RSM) and the linear pressure-strain two-layer model (LPS-RSM). EB-RSM model applies only one scalar elliptic equation instead of the original six transport equations for all stress components, which is based on the relaxation formulations of the pressure-strain tensor using a blending function. In the LPS-RSM model, the pressure-strain term $\phi_{ij}$ comprises a slow term (also known as the return-to-isotropy term), a rapid term, and wall-reflection terms. The Reynolds stress models can predict complex flows with swirl rotation and high strain rates more accurately than eddy viscosity models.

Solve the RANS equations

The incompressible flow can be solved by the segregated solver for pressure-velocity coupling. The pressure-correction equation can be constructed from the continuity equation and the momentum equations. The SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm is used to solve the pressure and velocity for steady and unsteady problems. The PISO (Pressure-Implicit with Splitting of Operators) algorithm is applied for unsteady problems. The SIMPLE algorithm is summarized as follows.

• Set the boundary conditions.
• Compute the velocity and pressure gradients.
• Calculate the intermediate velocity $v^*$ field by solving the discretized momentum equation.
• Compute the uncorrected mass fluxes at faces.
• Solve the pressure correction equation, which is constructed from the continuity equation.
• Update the pressure field with the pressure correction.
• Correct the mass fluxes at faces.
• Correct the cell velocities using the gradient of pressure corrections.
• Update density due to pressure changes.
• Advancing to next step iteration.

Introduction

.eps is a common used format of images in academic writting. If you want to convert hundreds of .jpg or .png. formats to .eps, the command convert in Linux system provides a good solution.

ImageMagick

引言

英国是个老牌海军强国，曾拥有世界最强的海军舰队，先后击败西班牙、荷兰和法国，成为新的“日不落帝国”。日不落帝国，即The empire on which the sun never sets，指的是全天任何时候都有领土或海外殖民地处于白昼，出自西班牙国王卡洛斯一世：在我的领土上，太阳永不落下。

1660年5月，查理二世继位，英国恢复君主制，并在同年成立了英国皇家海军和英国皇家学会。在大名鼎鼎的英国皇家海军里面，随便挑几个，无畏号、胡德号、厌战号、胜利号、光辉号等等，都是闪闪发光的名字。本文要讲的故事的主角不算最有名的那一档，但也实打实是一艘名舰。如果你去过伦敦，看过白金汉宫和泰晤士河上的伦敦塔桥（Tower Bridge)，那一定记得，有个略微破坏浪漫气息的军舰静静地停靠在市政厅旁边，她就是贝尔法斯特号轻巡洋舰，现已是帝国战争博物馆（Imperial War Museum）。大英帝国什么奇珍异宝没见过，为什么要把一艘退役军舰摆到伦敦最显眼的位置呢？她够格吗？

Introduction

Shell scripting makes life more comfortable. The command sequences of Linux can be combined in one shell script and be executed automatically without wasting any time. For example, if you would like to rename 9,999,999 files and put them into different directories during one week, clicking the mouse will be devastating. By shell scripting, all you need is to run one command in a loop. After that, you can have a vacation and enjoy coffee in the next seven days.

Suppose we have known at least a little bit about Linux. What is a Linux shell? Shell is an command language interpreter that executes commands. The most commonly used shells are SH (Bourne SHell) and Bash (Bourne again shell), released in 1989. Bash is not a perfect scripting language, but it is very useful. Life is short, get rid of the mouse.